반응형
문제
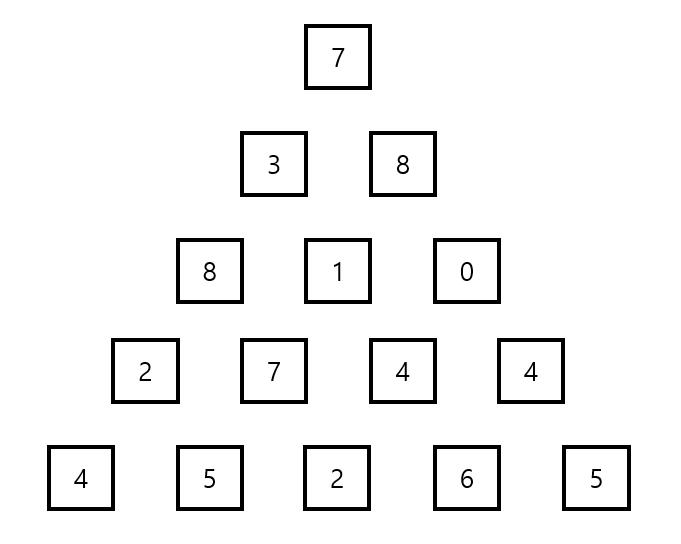
위 그림은 크기가 5인 정수 삼각형의 한 모습이다.
맨 위층부터 시작해서 아래에 있는 수 중 하나를 선택해 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하시오. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중 하나만 선택할 수 있다.
풀이
금광 문제와 마찬가지로 최대를 저장하는 2차원배열은 선언한다.
금광은 모든 2차원 배열을 탐색하면서 지나갔지만, 위 문제는 범위에 대한 조절만 잘 하면 된다.
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[][] graph = new int[n][n];
int[][] d = new int[n][n];
for (int i = 1; i <= n; i++) {
for (int j = 0; j < i; j++) {
graph[i-1][j] = sc.nextInt();
}
}
d[0][0] = graph[0][0];
int[] dy = {-1, 0}; // 왼쪽 대각선, 오른쪽 대각선
for (int i = 2; i <= n; i++) {
// d[i][j] => d[i][j] , graph[i][j] + d[i-2][j, j-1]
// 행의 길이는 윗 행보다 1 크다
for (int j = 0; j < i; j++) {
for (int k = 0; k < 2; k++) {
int ny = j + dy[k];
if (0 <= ny && ny < i-1) {
d[i-1][j] = Math.max(d[i-1][j], graph[i-1][j] + d[i-2][ny]);
}
}
}
}
int result = 0;
for (int i = 0; i < n; i++) {
result = Math.max(result, d[n-1][i]);
} //마지막 행에 각 루트의 최대값이 저장되어있다.
System.out.println(result);
}
}'Algorithm' 카테고리의 다른 글
| [Algorithm] 병사 배치하기 (0) | 2021.06.24 |
|---|---|
| [Algorithm] 퇴사 (0) | 2021.06.23 |
| [Algorithm] 금광 (0) | 2021.06.21 |
| [Algorithm] 공유기 설치 (0) | 2021.06.20 |
| [Algorithm] 고정점 찾기 (0) | 2021.06.19 |